Associated or induced $G$-connection
Now, observe that a principal bundle connection $\Gamma$ in a principal bundle produces a fiber bundle connection in the associated bundles. Take the context given in the latter note. Given $w \in E=(P\times F)/G$, take a representative $w=[u,\xi]$. We have a map
$$ \beta_{\xi}: P\longrightarrow E $$being $\beta_{\xi}(v)=[v,\xi]$. Now, take as definition:
$$ H_w:=d(\beta_{\xi})_u(H_u) $$At this way, we also carry the parallel transport concept to the associated bundle. \cite{goldberg}
Particular case: vector bundle connections
In the case of a vector bundle connection with associated principal bundle the frame bundle, the induced connection is obtained, in the sense of its connection 1-form, by simply pulling back with a particular frame. Let's see in the case of the tangent bundle.
Suppose we have a vector bundle connection $\nabla$ on the bundle $TM \to M$, induced by a principal connection on the frame bundle $FM \to M$ which is described by a 1-form on $FM$, $\tilde{\Theta}$. Then, if we select the frame $p=\{e_i\}$ in $M$, we are providing a section $p$ of $FM$, and we can consider the $\mathfrak{gl}(n)$-valued 1-form $p^*(\tilde{\Theta})$ on $M$.
On the other hand, the frame $p$ let us to write down a connection matrix $\Theta$ (whose entries are 1-forms) for the connection $\nabla$. Given a vector field $X$ on $M$, the connection $\nabla$ gives us a way to differentiate it:
$$ \nabla_X e_i = \sum_j \Theta^j_i(X) e_j $$
Where $\Theta^j_i(X)$ are the components of the $\mathfrak{gl}(n)$-valued 1-form $\Theta$ for the given frame.
Claim:
$$ p^*(\tilde{\Theta}) = \Theta. $$How does $p^*(\tilde{\Theta})$ acts on $X$?
Consider a point $p\in M$, we have
$$ p^*(\tilde{\Theta})(X_p)=\tilde{\Theta} (p_*(X_p)). $$Now, since $\tilde{\Theta}$ is the connection induced by $\Theta$, you can compute $\tilde{\Theta}(V)$ for a vector $V\in T_f(FM)$, and $f\in FM$ such that $\pi(f)=p$ and $d\pi_f(V)=X$. What $\tilde{\Theta}(V)$ does is consider $V$ as an infinitesimal curve in $FM$ $(p(t),v_1(t),v_2(t),\ldots)$ and extract the components of $\nabla_X v_1,\nabla_X v_2,\ldots)$.
But in the case $V=p_*(X_p)$, this curve is precisely $(p(t),e_1(t),e_2(t),\ldots)$ so
$$ \tilde{\Theta} (p_*(X_p))=\Theta(X_p). $$Conversely
In the case of $G=GL(n)$ there is a converse. Any linear connection on a vector bundle $E$ is induced from a unique principal connection on the frame bundle. See this answer in Mathstackexchange or @cap2009parabolic page 42.
Special (and important) case: when the principal bundle is the frame bundle and the associated bundle is the tangent bundle. There is an good reflection in the note connections summary.
Curvature
In the context given above. The curvature of the frame bundle is given by
$$ \tilde{\Omega}=d\tilde{\Theta}+\frac{1}{2}[\tilde{\Theta},\tilde{\Theta}] $$and the curvature curvature of the connection on the tangent bundle , in the frame $p$, is
$$ \Omega=d \Theta-\Theta \wedge \Theta $$It is clear that if $\tilde{\Omega}=0$ then $\Omega=0$. I think that the opposite is also true:
Given two vectors $V,W\in T_f FM$ with $d\pi(V)=X,d\pi(W)=Y$, $X,Y\in T_pM$ they can be interpreted as infinitesimal curves $\tilde{\alpha},\tilde{\beta}$ through $f$, i.e., curves $\alpha,\beta$ inside $M$ with moving frames over them. I guess that by means of a local trivialization we can find a local section $p:M \to FM$ such that restricted $\alpha,\beta$ we obtain the frames represented by $V,W$, that is,
$$ p_*(X)=V, \quad p_*(Y)=W. $$And then,
$$ \tilde{\Omega}(V,W)=\tilde{\Omega}(p_*(X),p_*(Y))=p^*(\tilde{\Omega})(X,Y)=\Omega(X,Y)=0. $$Example
(xournal 197)
Consider the worked example here, where we construct the connection 1-form of a connection on the tangent bundle of $\mathbb R^2$ from a covariant derivative operator $\nabla$. Now, let's see how to express the induced principal connection on the frame bundle in terms of its 1-form. Consider a frame $f\in FM$ at $p=(x_1,x_2)$. Since $FM$ is in this case $Aff(2)=\mathbb R^2\rtimes GL(2)$ it can be seen as a subgroup of $GL(3)$ and then
$$ f= \begin{pmatrix} c_{11} & c_{12}& x_1\\ c_{21} & c_{22}& x_2\\ 0 & 0& 1\\ \end{pmatrix} $$The first components of the columns are elements of $\mathbb R^2$. If we pass from a frame $f$ at $p$ to a frame $f'$ at $p'$ the 1-form of the connection measures how this change fails to be constant.
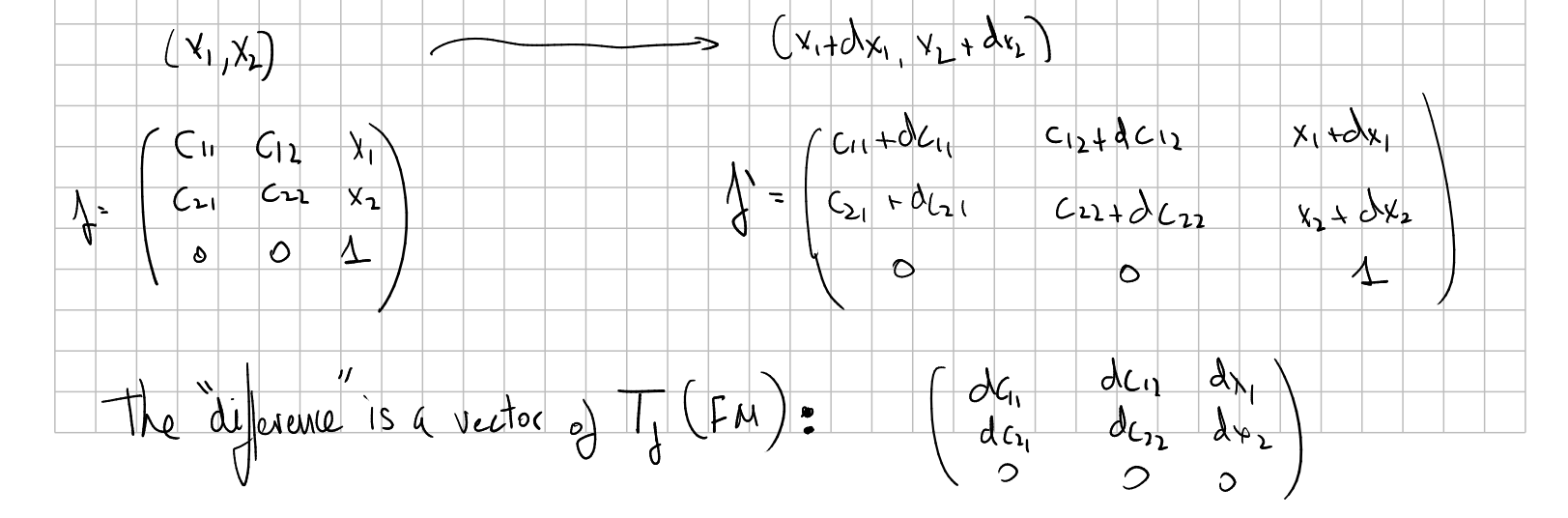
To compute the 1-form we apply the 1-form of the original vector bundle connection (see here) to the vectors
$$ \begin{array}{c} e_1:=(dx_1,dx_2,dc_{11},dc_{21})\\ e_2:=(dx_1,dx_2,dc_{12},dc_{22})\\ \end{array} $$to see how every vector in the frame fails to be constant.
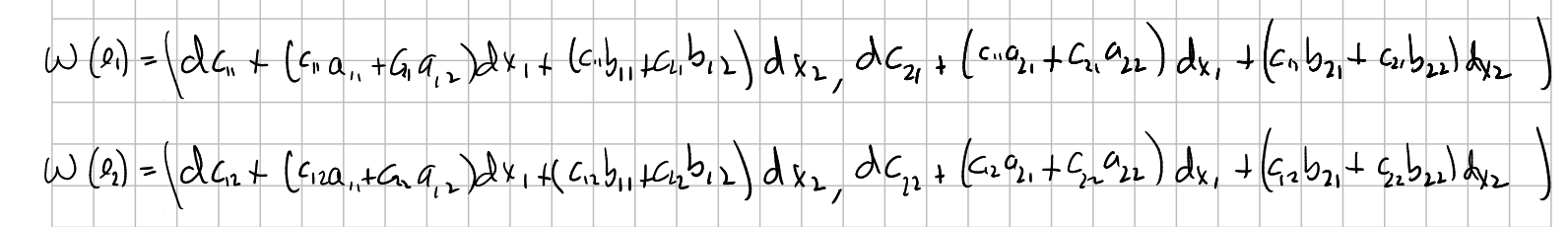
These "mistakes" are expressed like an element of $V_f FM$. But in order to compare the mistakes, we "send them" to a common place, $V_e FM$ being $e$ the origin with the canonical basis, or, equivalently, to $\mathfrak{gl}(2)$. I have to think this better. Anyway, what we are doing is to express these mistakes with respect to the frame $f$ itself, so we multiply the matrix
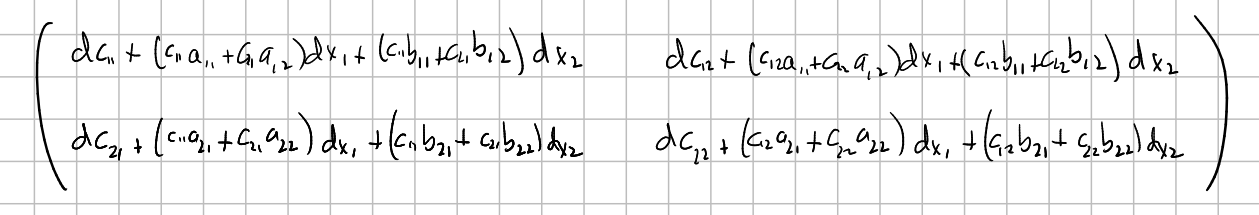
made with the mistakes by $C^{-1}$ obtaining $\omega\in \Omega(FM)\otimes \mathfrak{gl}(2)$:
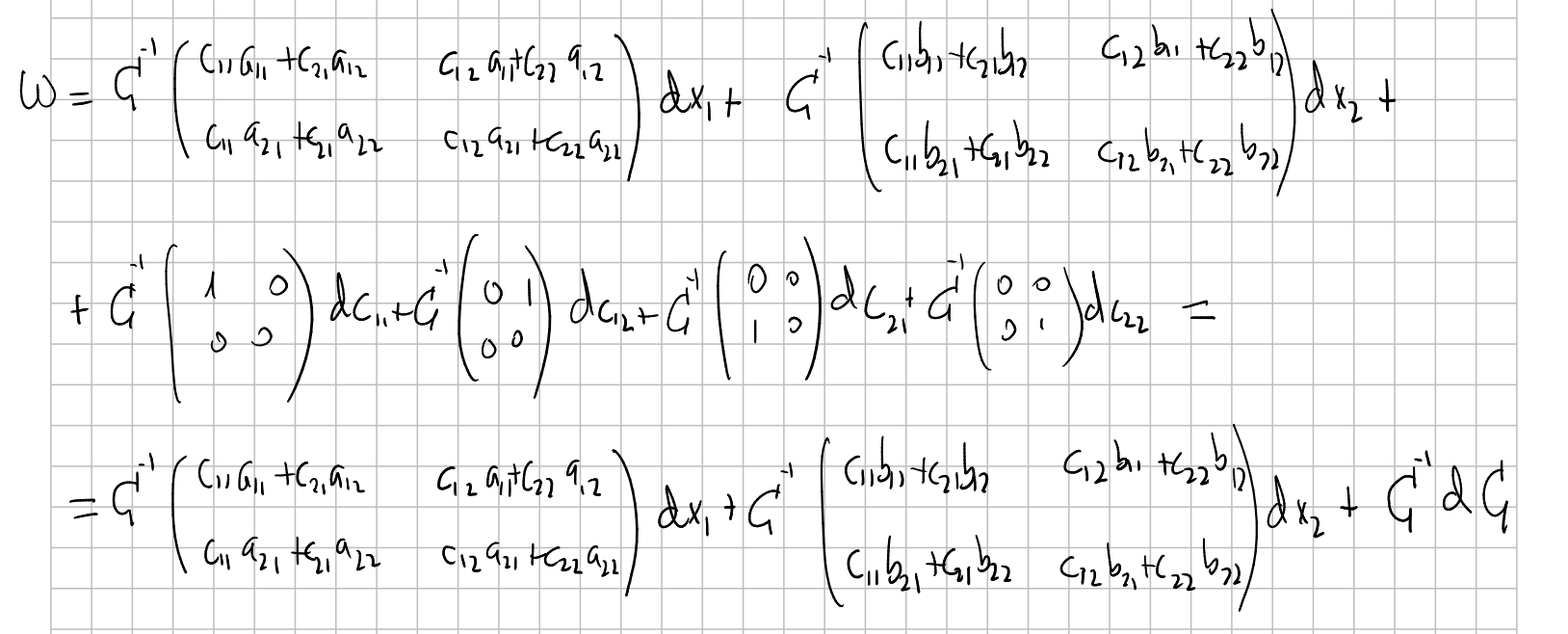
being $C$ such that
$$ f= \begin{pmatrix} C & p\\ 0 & 1\\ \end{pmatrix} $$Remember: this 1-form tells us how much do we "fail to be constant" when we pass from the frame $f$ to a nearby frame $f'$, but expressing this mistake with respect to the frame $f$ itself.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: